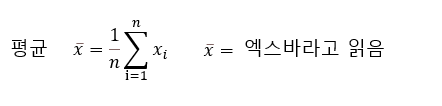오늘도 블로그

 확률변수(確率變數, random variable) 

어떠한 값이 되는가 하는 것이 확률 법칙에 의해 결정되는 변수를 확률변수 (random variable) 라 한다.  

• 값이 이산적(離酸的, dirscrete) 일 때, 이산형(離酸形) 확률 변수 
• 값이 연속적(連續的, continuous) 일 때 , 연속형(連續形) 확률변수라 한다.

확률변수라는 총체적인 의미를 나타낼 때에는  X와 같이 대문자로 나타내고, 확률변수의 표본값(데이터)으로서 실제값을 나타낼 때에 x와 같이 소문자로 나타내는 것이 일반 적인 표현 방법이다. 

확률밀도함수(確率密度函數ㅡ probability density function, p.d.f)

 확률변수 X 가 a ≤ X ≤ b의 값을 가지는 확률 P(a ≤ X ≤ b)가 

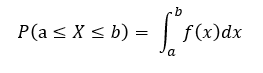
와 같이 나타낼 수 있을 때, f(x)를 확률밀도함수(確率密度函數ㅡ probability density function)라 한다. 

f(x)에는 다음과 같은 성질이 있다. 

 반대로 이 두 조건을 만족하는 함수는 모두 확률밀도함수가 될 수 있다. 

위 그래프 "1.확률밀도 함수"의 확률을 도식적으로 나타내면  아래  (a)의  빗금친 부분의 면적에 해당하며,  특히 어떠한 특정한 값 x를 가질 확률은, 식 "2.확률밀도 함수의 성질" 과 같이  a와 b를 한없이 x 값에 접근 시킨 경우의 값으로 얻어지며, (b)와 같이 x에서 dx 를 생각하여 x와 x+dx 사이의 확률 f(x)dx 로 정의 할수 있다. 

  확률 밀도 함수 이것만 보면,  무엇을 설명 하고 싶은 건지 알수 없다.  

 아래의 예제를 보면 확률밀도 함수의 구간을 구하는 코드가 있다.  확률밀도 함수는 0~1까지의 숫자로 나타내며,  그 합이 1이여야 한다.    결국 확률 100% 넘지 못한다는 것이다.   구간으로 따지면   0 ≤ x ≤ 1 이다.   아래는 평균이 0이고 표준편차가 1인 정규분포의 밀도함수를 그린 것이고,  -2 ≤ x ≤ -1 까지의 구간을 빗금 친 것이다. 

# 평균이 0이고 표준편차가 1인 정규분포의 밀도함수를 만든 
# 이후 -2 부터 -1까지의 확률 밀도 함수의 그래프 구간을 그리면
  
  par(mfrow = c(1, 1))
  x <- seq(-3, 3, length = 100)
  y <- dnorm(x)
  plot(x, y, type = "l")

  xlim <- x[-2 <= x & -1 >= x] 
  ylim <- y[-2 <= x & -1 >= x]

  xlim <- c(xlim[1], xlim, tail(xlim, 1))
  ylim <- c(0, ylim, 0)
  
  polygon(xlim, ylim, density = 20)

        데이터 분석을 하거나,   머신러닝,  딥러닝 종류의  분석을 하려면,  통계학은 기본적으로 알고 가야 한다.   이것의 의미를 모르면,  어떠한 강의를 듣더라도 이해를 잘 못할 뿐 아니라,  어떠한 과제가 주어 졌을때,  기본적인 툴만 사용해서 해석 하는 Tooler 가 될수 있다. 

  Tooler 가 되면,  모든 분석에 있어서  Overfitting과  Underfitting에 대한 해석을 못해  분석 후 시스템에 적용시, 모델 결과 값은 좋은데,  실무에 적용하기 어려운 케이스가 매우 많다. 

모집단(母集團, pupulation)과 표본(標本, sample)

 어떠한 사물의 특징이나 현상을 알 필요가 있는 경우가 많다.  이러한 경우 일반적으로 관찰이나 측정을 해야 한다.  이러한 관찰이나 측정의 대상이 되는 사물이나 현상의 전체를 모집단(母集團, pupulation)이라고 한다. 

그러나 특별한 경우를 제외하고 모집단의 양이 너무 커서 모집단 전체를 관찰하거나 측정 하는 것은 거의 불가능 하다. 

실제로 관찰하기 위해 측정된 일부를 표본(標本, sample) 이라고 한다. 

표본을 가지고 올때,  우리는 샘플링 하여, 표본을 가지고 온다.  보통 샘플링 할때는 우리는 Random 하게 샘플링하여 데이터를 추출 하는 경우가 많다. 

흩어짐(dispesion)과 분포(分布, distribution)

  어떠한 대상을 측정 하였을 경우, 얻어지는 측정값은 언제나 일정한 하나의 값이 아니고, 각각 다른 값이 되는 것이 일반적이다.  이렇게 측정값의 크기가 고르지 않은 것을 흩어집(dispersion)이라 하고,  이 흩어짐의 상태를 분포(分布, distribution)라고 한다. 

표본평균(標本平均, sample mean)과 표본분산(標本分産, sample variance) 

  측정치의 크기는 일반적으로 다르므로 어떠한 분포를 사용하게 된다.  측정치의 분포상태를 정량적으로 나타내면 비교 등에 매우 편리하다. 

  분포상태를 나타내는 특성 중, 가장 중요한것이 1) 분포의 중심과 2) 흩어짐 정도 일것이다. 

분포의 중심을 나타내는 양으로서 평균값이 사용되며,  표본에 대해서는 다음과 같이 산술(算術)평균으로 얻어 진다.  

아래와 같은 기호를 사용하며,  "바" 라고 부른다. 

흩어짐의 정도를 나타내는 것은 평균값에서 값이 어느정도 떨어져 있는 가에 대한 것은로  데이터 양이 흩어짐의 정도를 나타낸 것을 분산(分産, variance) 라 한다. 

예제 ) 평균 및 분산 

   어느 야구선수의 15년간 평균 홈련 데이터를 나타낸 것이다.  홈련의 평균과 분산을 R로 구현 하여라.   

> # 홈련값의 변수를 x라고 한다. 
> x = c(24, 22, 26, 24, 18, 25, 24, 23, 24, 20, 26, 25, 21, 27, 29)
> plot(x)
> # 평균값을 구한다. 
> mean(x)
[1] 23.86667
> #분산을 구한다.
> var(x)
[1] 7.838095

 공식은 조금 복잡 하지만, 평균은 mean() 함수를 사용하고 분산은 var() 함수를 사용한다. 

치우침(bias)

  어떠한 측정 대상이 값이 하나의 값이라 해도, 많은 회수를 측정을 하면 측정 값 언제나 하나의 값으로 측정되지 않고, 여러 값으로 측정 되는 것이 일반적이다.  이 때, 측정치 분포의 중심, 즉 평균값과 참값과의 차이를 치우침(bias)라 한다. 

참값

 원래 참값이란 모르는 값이나 측정 분야에서는 참값을, 대상이 되고 있는 양이 모범적인 방법(exemplar method), 즉 얻어진 데이터가 궁극적으로 사용될 목적에 대해 충분히 정확하다고 전문가들이 동의한 방법에 의해 측정되었을 때 얻어지라고 생각되는 값으로 보고 있다.